파스칼 삼각형
$(a+b)$
$(a+b)\times(a+b)$
$(a+b)\times(a+b)\times(a+b)$
......
의 전개식에서 각항의 계수만을 차례로 나열하면 삼각형 모양을 얻게 된다. 이와같이 이항계수를 나열한 것을 '파스칼 삼각형'이라고 한다.

파스칼 삼각형에서는 여러 가지 성질을 발견할 수 있다. 그 중 '하키 스틱 패턴'이라 불리는 다음 항등식에 대해 생각해 보자.
$C(r,r)+C(r+1,r)+\cdots+C(n,r) = C(n+1,r+1)$
이것 또한, 조합적으로 증명한다.
서로 다른 $(n+1)$개의 대상 $1, 2, \cdots, (n+1)$에서 $(r+1)$개를 선택하여 담은 임의의 한 상자를 X라 하자. 첫번째, $1$이 X에 속하는 경우, X를 만들기 위해서는 $1$을 제외한 나머지 수로부터 또 다른 $r$개를 선택하면 된다. 따라서 이 경우 상자 X를 만들어 내는 방법은
$C(n,r)$
가지가 있다. 두 번째, $1$은 X에 속하지 않으며 $2$가 X에 속하는 경우, X를 만들기 위해서는 $1$과 $2$를 제외한 나머지로 부터 또 다른 $r$개를 선택하면 된다. 따라서 이 경우 상자 X를 만드는 방법은
$C(n-1,r)$
이다. 이것을 계속 진행하면, $(n+1-r)$번째에서
$1, 2, \cdots , (n-r)$
은 A에 속하지 않으며 X를 만드는 방법에는
$C(r,r)$
가지가 있다. 위의 $(n+1-r)$가지의 경우는 서로 동시에 일어날 수 없으므로 '합의 법칙'에 의해 주어진 항등식은 성립한다.
다음의 경우에 대해서도 성립한다. 모든 자연수 $r, k$에 대해,
$C(r,0)+C(r+1,1)+\cdots+C(r+k, k)=C(r+k+1,k)$
이다. 이것은 파스칼 삼각형의 대칭성으로 인해 두 항등식은 사실상 동치이다. 시각적으로 이것이 보여지는가?
특별한 능력이 필요한 것은 아니다. 파스칼 삼각형을 자세히 바라보면 보일 것이다.
'하키 스틱 패턴'이라 불리는 항등식이 어떻게 활용될 수 있는지 다음 예제를 통해 알아본다.
정삼각형 $\rm ABC$의 $n-$분할을 다음과 같이 정의하자.
(1) 정삼각형 $\rm ABC$의 각 변 위에 등간격인 n개의 점을 주어 $(n+1)$개의 선분으로 나눈다.
(2) 세 변위의 $3n$개의 점들의 쌍을 나머지 하나의 변에 대해 평행이 되므로 $3n$개의 선분을 긋는다.
여기서 정삼각형의 $n-$분할에 포함된 평행사변형의 개수를 $g(n)$이라 하자. $g(1)=3$, $g(2)=15$, $g(3)=45$임을 확인할 수 있다. 정삼각형 $\rm ABC$의 $2-$분할은 다음 그림과같다.

이것을 일반화시켜 문제를 생각해 보자. $g(n)$에는 다음 그림과 같은 3가지 종류(왼쪽부터 1형, 2형, 3형)의 평행사변형이 있다.

대칭성에 의하여 각 종류의 평형사변형의 수는 같다. 그러므로 우리는 한 가지 종류의 평행사변형의 수를 계산하면 된다. 여기서는 1형의 평행사변형의 수를 계산한다.

정삼각형 $\rm ABC$의 각 변은 $n+1$의 단위선분들로 이루어져 있다.
꼭지점 $\rm A$로부터 d(1)까지의 거리가 단위선분 $1$개라면, d(2)를 선택할 수 있는 가짓수는 $n$개이고, 또 그의 짝 {d(3),d(4)}를 선택하는 가짓수는
$1=C(2,2)$
가지이다.
꼭지점 $\rm A$로부터 d(1)의 거리가 단위 선분 $2$개라면, d(2)를 선택할 수 있는 가짓수는 $(n-1)$개이고, 또 그의 짝 {d(3),d(4)}를 선택하는 가짓수는
$C(3,2)$
이다.
이와 같은 방식으로 꼭지점 $\rm A$로부터 d(1)의 거리가 단위 선분 $r(=1,2,\cdots,n)$개라면, d(2)를 선택할 수 있는 가짓수는 $(n+1-r)$개이고, 또 그의 짝 {d(3),d(4)}를 선택하는 가짓수는
$C(r+1,2)$
이다.
그러므로 구하고자 하는 1형-평행사변형의 총 개수는 다음과 같다.
$C(2,2)\times n + C(3,2)\times(n-1)+C(4,2)\times(n-2)+\cdots+C(n+1,2)\times1$
$= C(n+2, 3)+C(n+1,3)+\cdots+C(4,3)+C(3,3)$
$= C(n+3, 4)$
그러므로 $g(n) = 3C(n+3,4)$이다.
$g(n)$에 대한 위의 해답이 간단한 이항계수의 형태로 나타난 것에 착안해 보면 좀더 세련되거나 직접적인 조합적 방법이 있을 것 같다.
이 방법은 매우 심플하다.
여기서는 편의상 2형의 평행사변형을 세어본다. 정삼각형 $\rm ABC$에서 $\rm AB$와 $\rm AC$의 변을 연장하여 정삼각형 $\rm AB'C'$을 만든다. 이때 삼각형 $\rm AB'C'$은 $(n+1)$분할이 된다. 선분 $\rm B'C'$ 위에 $\rm B'$와 $\rm C'$를 포함해서 $(n+2)$의 점이 있음을 알 수 있다.
이제 아래 그림과 같이 정삼각형 $\rm ABC$의 $n-$분할에서 임의의 2형-평행사변형은 $\rm B'C'$ 위의 어떤 네 개의 점과 일대일 대응임을 관찰할 수 있다.
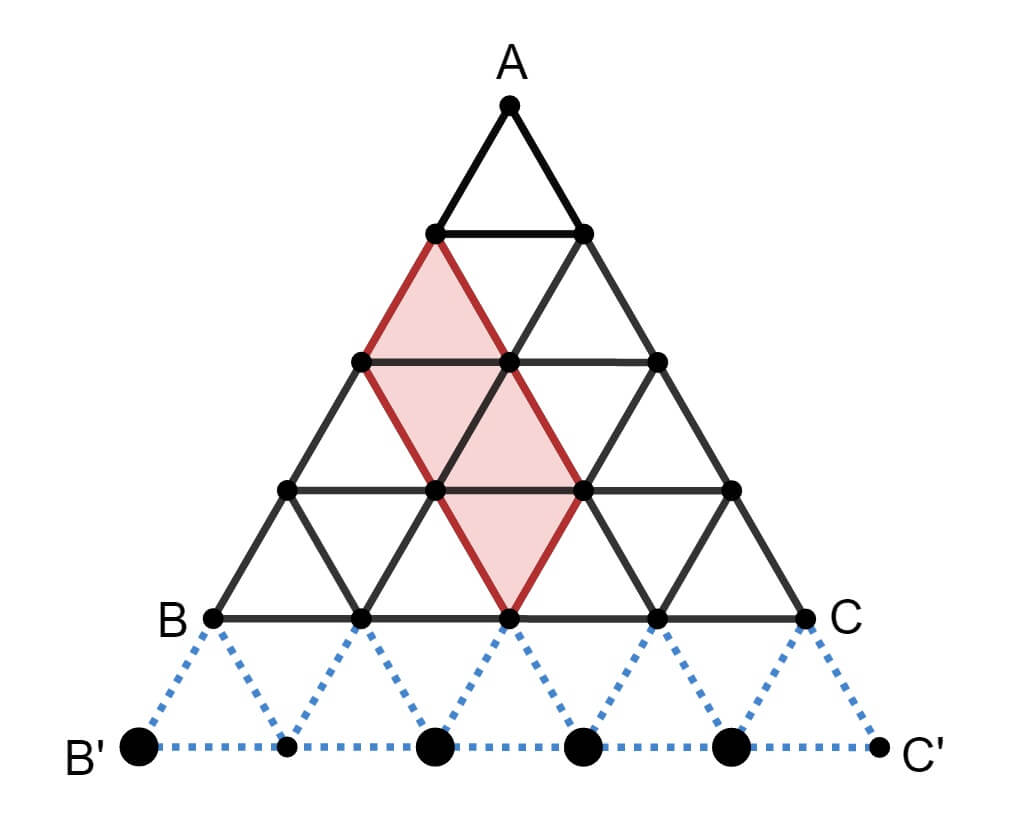
따라서 2형-평행사변형의 개수는 $C(n+3,4)$이고
$g(n)=3C(n+3,4)$
이다.
'Counting의 기술' 카테고리의 다른 글
| 2.4 다항계수 (0) | 2022.09.10 |
|---|---|
| 2.3 격자 직사각형에서의 최단경로 (0) | 2022.09.10 |
| 2.1 이항계수 (0) | 2022.09.10 |
| 2.0 제2장의 목차 (0) | 2022.09.08 |
| 1.7 분배문제 (0) | 2022.09.08 |




댓글